Conoce cuál es la utilidad del promedio, la desviación estándar y los percentiles, en los informes de pruebas de performance.

Hay ciertas métricas clave de pruebas de performance que es muy importante comprenderlas correctamente, para así sacar las conclusiones correctas de las pruebas.

Estas métricas requieren una comprensión básica de matemáticas y estadísticas, pero nada demasiado complicado. El problema es que si no comprende bien lo que significa cada uno o lo que representan, llegará a conclusiones muy equivocadas. 

En este post, quiero centrarme en el promedio, la desviación estándar y los percentiles. Sin entrar en muchas matemáticas, discutiremos la utilidad de cada una de estas métricas al analizar los resultados de performance.

Importancia de analizar los datos como un gráfico

La primera vez que pensé en este tema fue durante un curso que impartió Scott Barber en 2008 (cuando recién estábamos iniciando Abstracta), en su visita a Uruguay. Nos mostró una tabla con valores como este:

Nos preguntó qué conjunto de datos pensamos que tenía la mejor performance, que no es tan fácil de discernir como cuando se muestran los datos en un gráfico:

En el conjunto A, se puede decir que hubo un peak, pero luego se recupera.

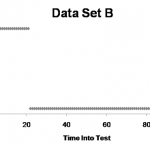
En el conjunto B, parece que comenzó con tiempos de respuesta pésimos y probablemente 20 segundos después de la prueba, el sistema colapsó y comenzó a responder con una página de error, que luego se resolvió en un segundo.

Finalmente, en el conjunto C, está claro que a medida que pasaba el tiempo, la performance del sistema continuaba con degradación.

El objetivo de Barber con este ejercicio era mostrar que es mucho más fácil analizar la información cuando se presenta en un gráfico. Además, en la tabla se resume la información, pero en las gráficas se pueden ver todos los puntos.

Por tanto, con más data points (marcadores), podemos obtener una imagen más clara de lo que está sucediendo.

Comprensión de las métricas clave de las Pruebas de Performance

Bien, ahora veamos qué significa cada una de las métricas de las pruebas de performance, y su importancia para fines de análisis.

1. Promedio

Para calcular el promedio, simplemente sume todos los valores de las muestras y luego divida ese número por la cantidad de muestras. Al hacer esto el promedio resultante es de 3 segundos. El problema con esto es que, al hacerlo al pie de la letra, brinda una falsa sensación de que todos los tiempos de respuesta son de unos tres segundos, algunos un poco más y otros un poco menos, pero puede que ese no sea el caso.

Imagine que tiene tres muestras, las dos primeras con un tiempo de respuesta de un segundo, la tercera con un tiempo de respuesta de siete:

1 + 1 + 7 = 9

9/3 = 3

Este es un ejemplo muy simple que muestra que tres valores muy diferentes podrían resultar en un promedio de tres, sin embargo, los valores individuales pueden no estar cerca de 3.

Mi colega, Fabián Baptista, hizo un comentario divertido relacionado con esto:

“Si pusiera una mano en un balde de agua a -100 grados Fahrenheit y la otra mano en un balde de lava ardiente, en promedio, la temperatura de mi mano estaría bien, pero perdería ambas manos”.

Entonces, al analizar los tiempos de respuesta promedio, es posible obtener un resultado que esté dentro del nivel aceptable, pero tenga cuidado con las conclusiones a las que llega.

Por eso, no se recomienda definir acuerdos de nivel de servicio (SLA) utilizando promedios; en lugar de eso, tenga algo como “El servicio debe responder en menos de 1 segundo en el 99% de los casos”. Veremos sobre esto más adelante con la métrica de percentiles.

2. Desviación Estándar

La desviación estándar es una medida de la dispersión con respecto al promedio, es decir, cuánto varían los valores con respecto a su promedio o qué tan separados están.

Si el valor de la desviación estándar es pequeño, esto indica que todos los valores de las muestras están cerca del promedio, pero si es grande, entonces están muy separados y tienen un rango mayor.

Para entender cómo interpretar este valor, veamos un par de ejemplos.

Si todos los valores son iguales, entonces la desviación estándar es 0. Si hay valores muy dispersos, por ejemplo, considere 9 muestras con valores de 1 a 9 (1, 2, 3, 4, 5, 6, 7, 8, 9), la desviación estándar es ~ 2.6 (puede usar esta calculadora online para calcularla).

Aunque el valor del promedio como métrica se puede mejorar enormemente al incluir también la desviación estándar, lo que es más útil aún son los valores de percentiles.

3. Percentiles

Un percentil es una métrica de prueba de performance muy útil, ya que proporciona una medida bajo la cual se encuentra un porcentaje de la muestra. Por ejemplo, el percentil 90 (abreviado como p90) indica que el 90% de la muestra está por debajo de ese valor y el resto de los valores (es decir, el otro 10%) están por encima de él.

Es práctico analizar más de un valor de percentil (JMeter y Gatling lo hacen en sus informes), mostrando cuántas muestras son p90, p95 y p99. Si estos se complementan con el mínimo, máximo y promedio, entonces es posible tener una visión mucho más completa de los datos y así entender cómo se comportó el sistema.

Algunos percentiles tienen nombres particulares, como p100, que es el máximo (el 100% de los datos está por debajo de este valor) y p50, que es la mediana (la mitad de los datos está por debajo y la mitad por encima).

El percentil se usa típicamente para establecer criterios de aceptación, lo que indica que el 90% de la muestra debe estar por debajo de cierto valor. Esto se hace para descartar valores atípicos.

Consideraciones clave

Entonces, antes de analizar los resultados de su próxima prueba de performance, asegúrese de recordar estas consideraciones clave:

• Nunca considere el promedio como “el” valor al que hay que prestar atención, ya que puede ser engañoso, dado que comúnmente oculta información importante.
• Considere la desviación estándar para saber qué tan útil es el promedio, cuanto mayor es la desviación estándar, menos significativa es.
• Observe los valores del percentil y defina los criterios de aceptación basados ​​en eso, teniendo en cuenta que si selecciona el percentil 90, básicamente está diciendo: “No me importa si el 10% de mis usuarios experimentan tiempos de respuesta malos” .

¿Qué otras consideraciones tiene al analizar las métricas de las pruebas de performance? ¡Cuéntenos en los comentarios!

---

Otros contenidos relacionados

Tipos de Pruebas de Performance

¿Cómo diseñar un Plan de Pruebas de Performance?

¿Cuándo es el mejor momento para comenzar con las Pruebas de Performance?